鹦鹉螺类是著名的活化石，早在几亿年前就出现了。作为四大名螺之一的鹦鹉螺，它们的整个螺旋形外壳光滑如圆盘状，形似鹦鹉嘴，故得名“鹦鹉螺”。它们在海洋里混的风生水起，一度稳坐海洋霸主之位。鹦鹉螺优美的外壳形状，符合斐波那契数列，也叫鹦鹉螺黄金分割，这种奇特的外形让它既有时间底蕴又具艺术审美。

从外形上看，鹦鹉螺的壳看起来更完美，完全左右对称；而任何一个螺壳都是螺旋不对称的。壳外呈灰白色，有很多细的生长纹，夹杂橙红色波状粗条。再看硬壳里面有很多分格，只有最外面一格是供它居住的，叫住室。里面的结构叫做气室，它们通过一根体管连接，主要是用来调节自身浮力的。通过改变气室内的气液比例，鹦鹉螺可以实现在垂直方向上的上浮下潜。

早期的潜水艇就是仿照了鹦鹉螺的原理进行的设计

正是因为这种特殊的身体构造，才能让鹦鹉螺在深海中“出入自由”！鹦鹉螺通过连接各个壳室（气室）的小管吸入或者排出海水来调节全体的比重而浮沉。聪明的人类正是利用这个原理，创造了潜艇。

鹦鹉螺号潜艇

我们知道，黄金分割线是一种古老的数学方法，黄金分割的创始人是古希腊的毕达哥拉斯，他在当时十分有限的科学条件下大胆断言：一条线段的某一部分与另一部分之比，如果正好等于另一部分同整个线段的比即0.618，那么这样的比例会给人一种美感。那么，黄金分割曲线又是什么呢？

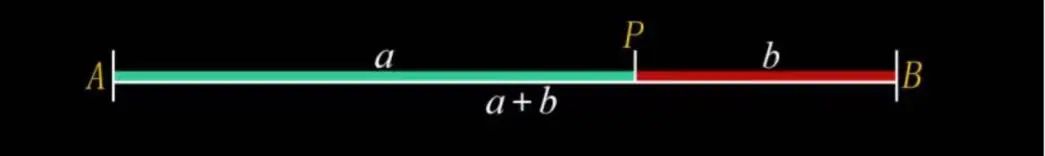
感兴趣的小伙伴可以拿出纸和笔，根据以下的步骤便可以画出一个鹦鹉螺的轮廓：先画两个边长为1的正方形，再画边长为2的正方形、边长为3的正方形、边长为5的正方形……我们可以得到一个长宽比约为0.618的矩形。而每个正方形边长所组成的数列：0、1、1、2、3、5、8、13、21、34……即为斐波那契数列。

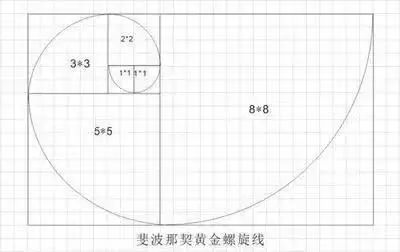
更为神奇的是，如果我们把每个正方形中90°的扇形曲线依次连接起来，便可得到一个螺旋曲线——斐波那契螺旋线。其发散角为137.5°，我们用圆周角（360°）减去发散角便得到一个大小为222.5°的角，将二者进行比较，我们发现恰好也得到一个黄金分割数，这个螺旋线也被称为黄金螺旋线。

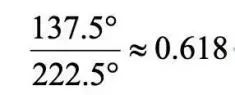
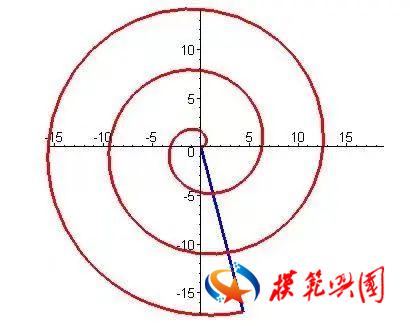
如果我们把这个曲线放到直角坐标系中，我们可以发现，它穿过原点的任意直线永远与螺线相交的角相等，每一圈螺纹的长度都等于里边两圈的长度之和。因此，这条完美螺线也被称为等角螺线或者对数螺线。

许多人相信，黄金分割反映的是宇宙万物的一种自身规律，德国数学家阿道夫·蔡辛（Adolf Zeising）认为，黄金分割是所有比例中最富艺术感的一种，他说：“宇宙之万物，凡符合黄金比例的总是最美的形体。”龙卷风、银河系中也蕴藏着黄金螺线的身影。

再比如向日葵花盘上呈现的顺时针和逆时针两种分布的曲线，数量通常是一对连续的斐波那契数（逆时针和顺时针曲线数量分别为34条、55条，34：55≈0.618），以及松果的曲线数量等。

许多植物相邻两片叶子约成137.5°，因为137.5：（360-137.5）≈0.618，此时采光、通风是最佳的。

怡人的气温会在23℃（37℃×0.618≈23℃），因为气温与体温构成黄金比例时，你我会感觉最舒适。

黄金比例是如此完美，又是如此神秘。如果说在人类社会，人们还可以刻意制造出黄金比例，那么在大自然中，那么多的黄金比例都是谁造就的呢？伽利略曾说：“数学似乎是上帝的语言。” 究竟是人创造了黄金分割还是大自然创造了黄金分割，这依然众说纷纭，莫说一是。

参考文献

[1]https://mp.weixin.qq.com/s/uFaCIGf0uT-FT_4P03c6eg

[2]https://mp.weixin.qq.com/s/Z3MIhs_HAy_RQjWRdZWfKg

[3]https://mp.weixin.qq.com/s/mA5gKt5XwwHuJ272PsBzYA

来源：力学科普

编辑：张宇   校对：敖雯菲

审核：张月华   何承健

监制：谢华容

总监制：魏凡翔